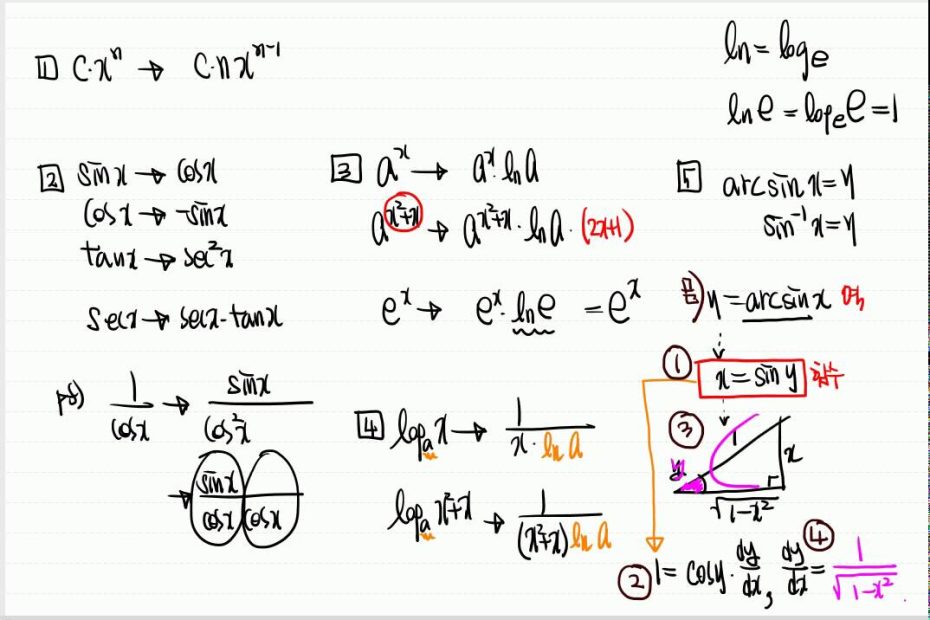
미적분 공식 쉽게 이해하기: 초보자를 위한 가이드 (Understanding Calculus Formulas: A Beginner’s Guide)

미적분 공식

미적분은 함수의 미분과 적분을 다루는 수학 분야이다. 미적분은 물리학, 공학, 경제학, 생물학에서 중요한 역할을 한다. 이 글에서는 미적분에서 많이 사용되는 공식들을 살펴보려고 한다.

미분 공식

미분은 함수의 증가율을 나타내는 것이다. 미분 공식은 다음과 같다.

1. 상수 함수: f(x) = c, (c는 상수)일 때, f'(x) = 0 이다.

2. 면적 함수: f(x) = x^n 일 때, f'(x) = nx^(n-1) 이다.

3. 지수 함수: f(x) = e^x 일 때, f'(x) = e^x 이다.

4. 로그 함수: f(x) = log(x) 일 때, f'(x) = 1/x 이다.

5. 삼각 함수: f(x) = sin(x) 일 때, f'(x) = cos(x) 이다.

적분 공식

적분은 함수의 면적을 계산하는 것이다. 적분 공식은 다음과 같다.

1. 면적 함수: f(x) = x^n 일 때, ∫f(x)dx = (1/(n+1))x^(n+1) + C 이다.

2. 지수 함수: f(x) = e^x 일 때, ∫f(x)dx = e^x + C 이다.

3. 로그 함수: f(x) = log(x) 일 때, ∫f(x)dx = xlog(x) – x + C 이다.

4. 삼각 함수: f(x) = sin(x) 일 때, ∫f(x)dx = -cos(x) + C 이다.

종합 공식

미분과 적분을 함께 사용하는 경우가 많다. 이때는 종합 공식을 사용한다. 종합 공식은 미분과 적분을 함께 이용할 수 있는 공식으로 다음과 같다.

∫(f(x)g'(x) + f'(x)g(x))dx = f(x)g(x) + C

FAQ

Q: 미적분은 어디에 사용될까요?
A: 미적분은 물리학, 공학, 경제학, 생물학 등 다양한 분야에서 사용됩니다.

Q: 미분과 적분의 차이는 무엇인가요?
A: 미분은 함수의 증가율을 나타내는 것이며, 적분은 함수의 면적을 계산하는 것입니다.

Q: 미분과 적분을 함께 사용하는 경우가 많다고 하는데, 어떤 경우에 사용되나요?
A: 예를 들어 미분한 결과를 적분하여 함수를 구하는 경우가 있습니다. 또한 적분한 결과를 미분하여 다른 함수를 구하는 경우도 있습니다.

Q: 미분과 적분을 배울 때 가장 어려운 부분은 무엇인가요?
A: 학생들이 가장 많이 어려워하는 부분은 공식을 이해하고 외울 때입니다. 그리고 차이점을 이해하는 것도 중요한데, 이는 연습을 통해 개선할 수 있습니다.

Q: 미적분은 해결하기 어려운 문제도 해결할 수 있나요?
A: 미적분은 해결하기 어려운 문제도 해결할 수 있습니다. 예를 들어 우주선이 중력장에서 이동할 때, 운동 방향과 속도를 계산할 때 미적분이 사용됩니다. 이외에도 여러 분야에서 문제 해결에 활용됩니다.

미적분 공식 주제와 관련된 36개의 이미지를 찾았습니다.

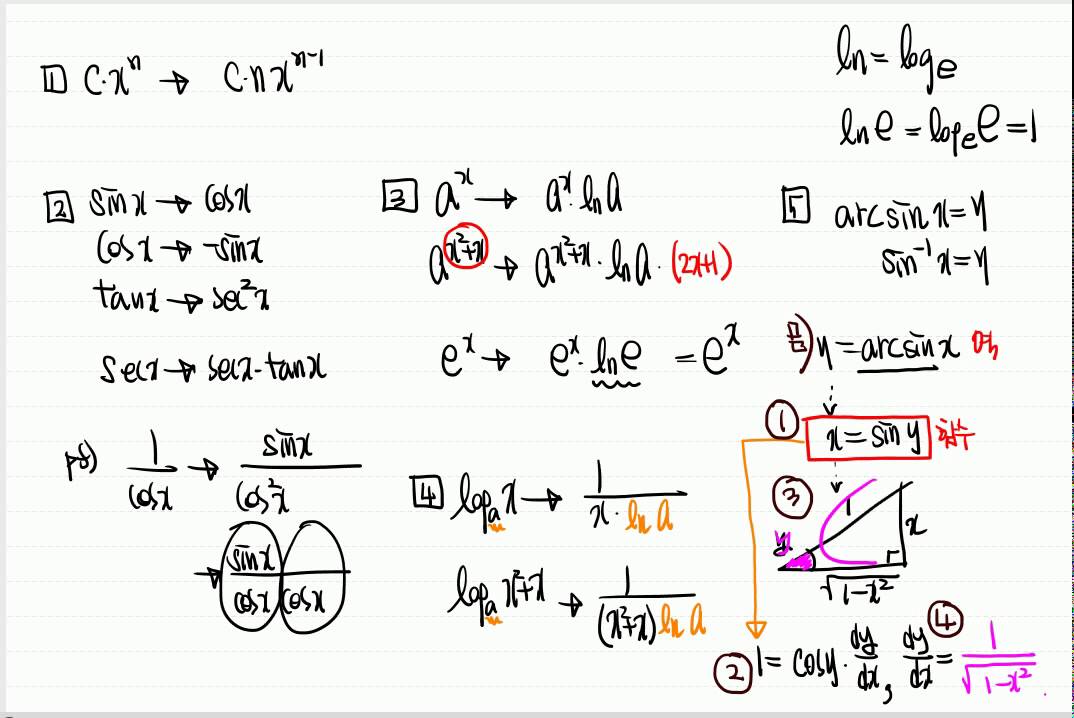
미적분은 수학에서 가장 중요한 분야 중 하나로, 고등학교 수준의 미적분 공식은 여러 분야에서 활용됩니다. 이 글에서는 고등학교 미적분 공식에 대해 정리하고자 합니다.

1. 미분법과 적분법

미분법은 함수의 변화율을 구하는 것으로, 즉 기울기를 구하는 것입니다. 미분의 기호는 f'(x)로 나타낼 수 있습니다. 적분법은 미분법의 반대 과정으로, 함수의 면적을 구하는 것입니다. 적분의 기호는 ∫f(x)dx로 나타낼 수 있습니다.

2. 미분의 기본 공식

미분의 기본 공식은 다음과 같습니다.

– 상수 함수: f(x) = c (c는 상수) → f'(x) = 0
– x의 거듭제곱 함수: f(x) = x^n (n은 자연수) → f'(x) = nx^(n-1)
– 상수배 함수: f(x) = cf(x) → f'(x) = cf'(x)
– 합의 미분: f(x) = g(x) + h(x) → f'(x) = g'(x) + h'(x)
– 곱의 미분: f(x) = g(x)h(x) → f'(x) = g'(x)h(x) + g(x)h'(x)
– 연쇄법칙: f(x) = g(h(x)) → f'(x) = g'(h(x))h'(x)

3. 적분의 기본 공식

적분의 기본 공식은 다음과 같습니다.

– 상수 함수의 적분: ∫c dx = cx + K (K는 상수)
– 거듭제곱 함수의 적분: ∫x^n dx = x^(n+1)/(n+1) + K (K는 상수)
– 상수배 함수의 적분: ∫cf(x) dx = c∫f(x) dx
– 부분 적분: ∫f(x)g'(x) dx = f(x)g(x) – ∫g(x)f'(x) dx

4. 적분의 치환법

적분의 치환법은 복잡한 함수를 간단한 함수로 치환하여 연산을 수행하는 방법입니다. 치환법에는 다음과 같은 종류가 있습니다.

– 대입법: 간단한 함수로 치환할 수 있는 경우 사용합니다.
– 삼각함수 치환법: 적분식에 삼각함수가 포함되어 있는 경우 사용합니다.
– 지수함수 치환법: 적분식에 지수함수가 포함되어 있는 경우 사용합니다.
– 로그함수 치환법: 적분식에 로그함수가 포함되어 있는 경우 사용합니다.

FAQ

1. 미분과 적분의 차이점은 무엇인가요?
미분은 함수의 변화율을 구하는 것으로 기울기를 구하는 것입니다. 적분은 미분의 반대 과정으로 함수의 면적을 구하는 것입니다.

2. 미분의 기본 공식은 어떤 것이 있나요?
미분의 기본 공식에는 상수 함수, x의 거듭제곱 함수, 상수배 함수, 합의 미분, 곱의 미분, 연쇄법칙 등이 있습니다.

3. 적분의 기본 공식은 어떤 것이 있나요?
적분의 기본 공식에는 상수 함수의 적분, 거듭제곱 함수의 적분, 상수배 함수의 적분, 부분 적분 등이 있습니다.

4. 적분의 치환법에는 어떤 종류가 있나요?
치환법에는 대입법, 삼각함수 치환법, 지수함수 치환법, 로그함수 치환법 등이 있습니다.

미분 공식 모음

미분(Differentiation)은 수학에서 함수가 어느 지점에서의 변화율, 순간 변화율을 구하는 과정입니다. 미분을 계산하기 위해서는 일련의 공식과 규칙을 알고 있어야 합니다. 이번 글에서는 미분 공식 모음을 소개하겠습니다.

1. 상수 함수의 미분 공식

y = c (c는 상수)라는 상수 함수가 있을 때, 그 함수의 미분값은 0입니다.

즉, dy/dx = 0

2. 차수의 공식

y = xn (n은 양의 정수)라는 차수 함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = nx^(n-1)

3. 상수곱의 공식

y = cf(x) (c는 상수)라는 함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = cf'(x) (f'(x)는 f(x)의 미분값)

4. 합의 공식

y = f(x) + g(x)라는 함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = f'(x) + g'(x)

5. 곱의 공식

y = f(x)g(x)라는 함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = f'(x)g(x) + f(x)g'(x)

6. 역함수의 공식

y = f^-1(x)라는 역함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = 1/f'(f^-1(x))

7. 지수 함수의 공식

y = e^x라는 지수 함수가 있을 때, 그 함수를 x로 미분하면 다음과 같은 공식을 사용합니다.

dy/dx = e^x

FAQ

Q1. 미분이 무엇인가요?
미분은 수학에서 함수가 어느 지점에서의 변화율, 순간 변화율을 구하는 과정입니다.

Q2. 미분의 응용 분야는 무엇인가요?
미분은 물리학, 공학, 경제학, 생물학 등 다양한 분야에서 응용됩니다. 예를 들어 물리학에서는 가속도와 속도, 거리와 시간의 관계를 나타내는 운동 방정식을 미분을 통해 유도할 수 있습니다. 경제학에서는 한 기업의 생산량이나 수익이 시간에 따라서 어떻게 변화하는지를 분석할 때 미분을 사용합니다.

Q3. 미분을 계산하는 방법은 어떤 것이 있나요?
미분을 계산하는 방법으로는 다양한 방법이 있습니다. 이번 글에서 소개된 공식 외에도, 미분의 정의를 직접적으로 적용하여 미분 값을 구할 수 있습니다. 또한, 미분을 계산하는 데 필요한 미적분학의 다양한 원리와 규칙들이 존재합니다.